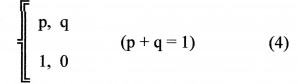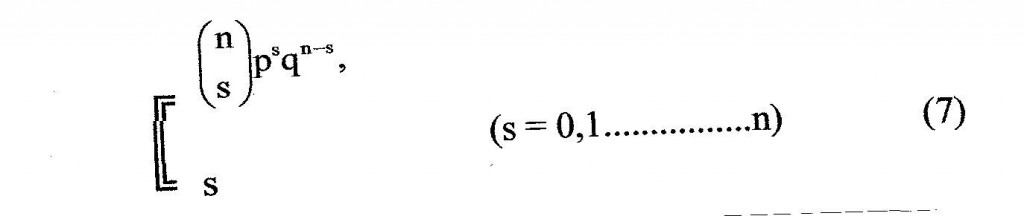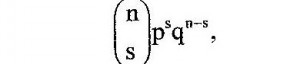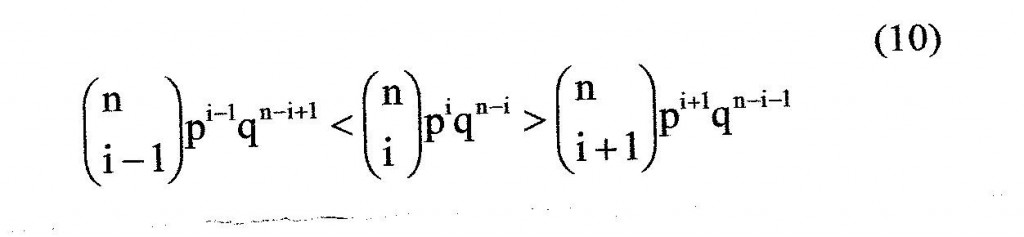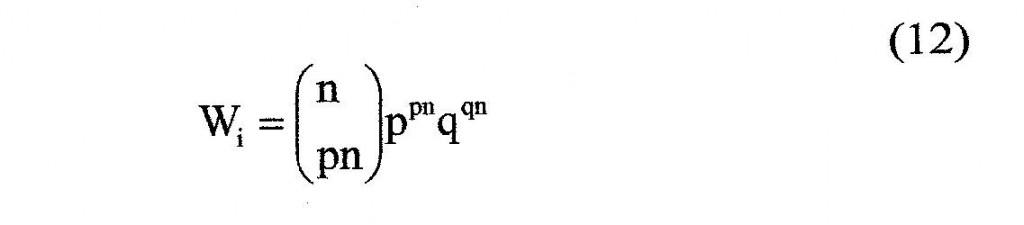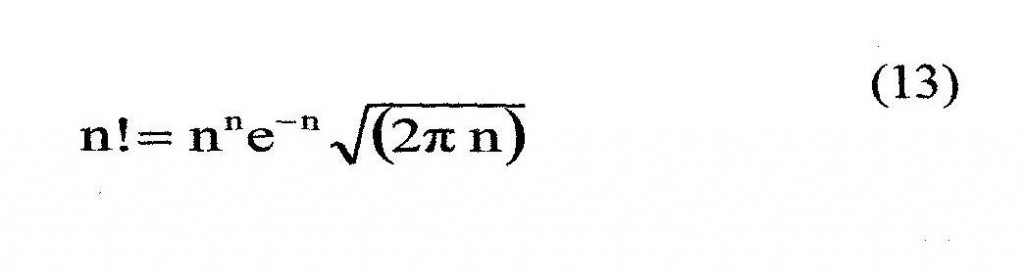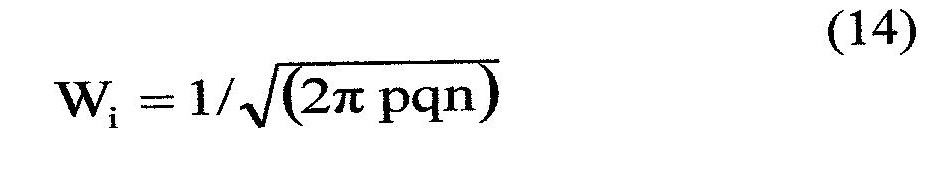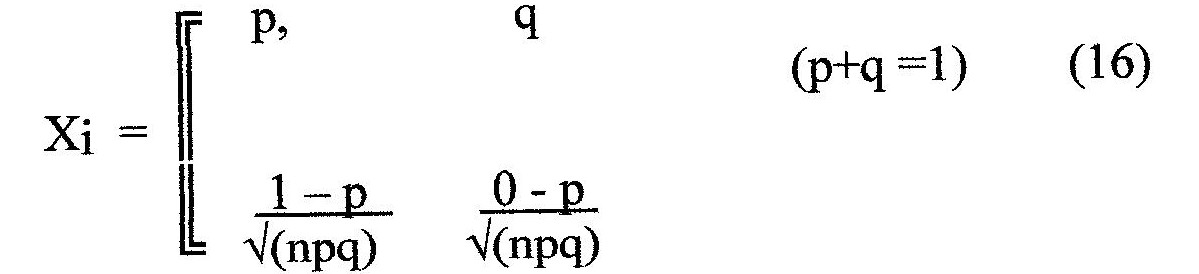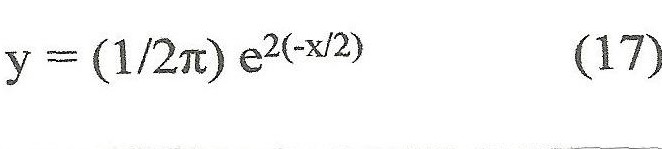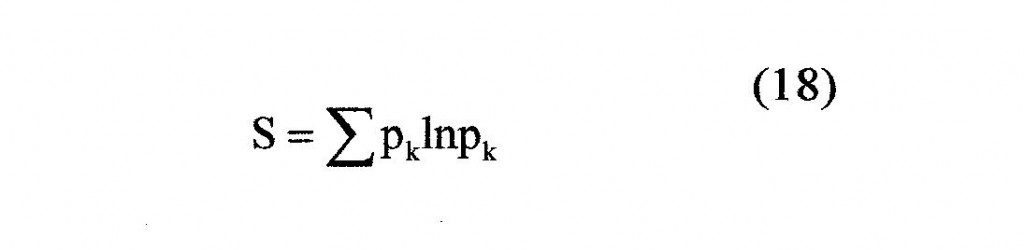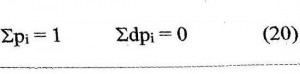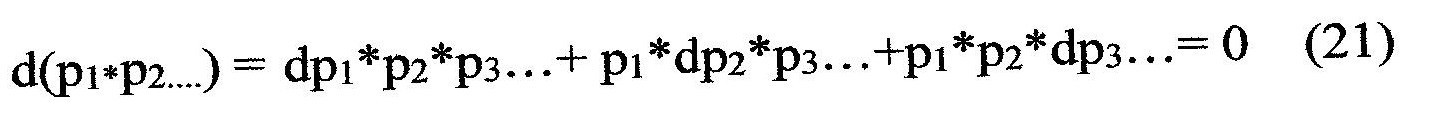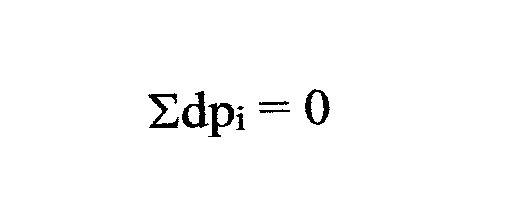Una delle leggi fondamentali della fisica statistica ha sollevato problemi di così difficile soluzione da bloccare, fino ad oggi, il progresso in campi di estremo interesse. Il mio proposito attuale è di mostrare, come questo fondamentale teorema potrebbe ricevere, sulla base di importanti avanzamenti della matematica statistica, delle profonde, sostanziali rielaborazioni. Intendo riferirmi alla legge sulla variabilità dell’entropia statistica di Boltzmann. Secondo Boltzmann, la configurazione di massima entropia ha la più alta probabilità di realizzarsi, ma non è la sola configurazione possibile. Quindi, il passaggio del sistema in equilibrio statistico attraverso configurazioni di minore entropia non è escluso (ipotesi ergodica).

Tale conclusione di Boltzmann è basata sull’ipotesi che i vari modi di combinazione dei microstati, che danno luogo alle varie configurazioni del sistema abbiano eguale probabilità. Per conseguenza, la configurazione di massima entropia ha la massima probabilità perché può essere ottenuta nel maggior numero di modi. Noi mostreremo, invece, che la configurazione di massima entropia è la sola possibile configurazione di una sistema in equilibrio statistico.

Iniziamo con il considerare il senso ed il significato che la statistica permette oggi di attribuire all’entropia statistica. Sia un sistema composto da n elementi estratti da un insieme più ampio e individuati da un indice i che va da 1 a n e supponiamo che tali elementi possano trovarsi in r stati individuati dall’indice k che va da 1 a r con probabilità p_i,k . E’ ovviamente:

∑p_k = 1            (1)

quale che sia l’elemento i considerato. Supponiamo anche che le probabilità siano eguali quale che sia l’elemento considerato, così che possano essere indicate semplicemente con p_k.

Poniamoci ora questa domanda: data tale struttura di probabilità dei componenti elementari, quale sarà la distribuzione più probabile degli n elementi?

Nello rispondere a questa domanda fondamentale, la statistica propone un contro-quesito preliminare che condiziona la soluzione del problema e i cui termini, pur essendo prospettati da oltre due secoli, non sono stati evidentemente compresi, visto che un errore banale nella risposta al contro-quesito è stato non solo commesso da Boltzmann ma non rilevato nel corso di un dibattito da allora mai interrotto.

Secondo la statistica, dunque, il termine di probabilità è privo di senso se non viene definito preliminarmente il campo di variazione nei cui confronti esso viene definito. Il campo di variazione può essere interno ad un insieme chiamato universo se costituito da un numero infinito di componenti e popolazione se costituito da un numero finito di componenti. In tal caso il campo di variazione è comune a tutti i componenti e si dice che esiste una interdipendenza statistica delle probabilità. Il campo di variazione nei cui confronti è definita la probabilità può essere invece interno ad ogni componente che può presentarsi in una molteplicità di modi alternativi, ed il campo di variazione complessivo per un insieme si costituisce per sovrapposizione moltiplicativa dei campi di variazione dei singoli componenti e si dice che esiste una indipendenza statistica delle probabilità.

Il caso tipico di interdipendenza statistica è costituito da una popolazione di individui classificati secondo una certa caratteristica, supponiamo il colore di una maglia indossata. La probabilità di un certo colore di maglia non costituisce una caratteristica variabile nell’individuo, che si presenta con un solo colore di maglia, ma è desunta dalla variabilità della caratteristica nella popolazione. Da notare, ai fini del raffronto con la condizione da cui è partito Boltzmann nelle sue elaborazioni, che la condizione di interdipendenza statistica non muta se gli individui si scambiano la maglia, perché il numero di maglie di un dato colore rimane in tal caso costante così come rimane per conseguenza costante la probabilità di ottenere un determinato colore di maglia scegliendo a caso un individuo dalla popolazione.

Se invece ciascun individuo può presentarsi con un colore diverso di maglia senza che ciò sia l’effetto di una scambio, ad esempio attingendo ad un campo di variabilità proprio, costituito dal proprio guardaroba, senza cioè che il numero di maglie di un determinato colore debba rimanere costante nella popolazione, si ottiene una condizione di indipendenza statistica delle probabilità.

Trasferiamo tali considerazioni al caso fisico che costituisce il punto di partenza della elaborazione di Boltzmann, vale a dire un gas monoatomico costituito da molecole fra le quali si esercitano solamente urti elastici e forze gravitazionali. Nell’ambito di valori costanti dell’energia complessiva e del volume complessivo del sistema, si avrebbe una condizione di indipendenza statistica delle probabilità degli stati delle molecole se ogni molecola potesse presentarsi in una molteplicità di stati indipendentemente dalla sua appartenenza al sistema. (Allo stesso modo di come un individuo, nell’esempio testé fatto, potrebbe mostrare, attingendo al proprio guardaroba, una variabilità del colore della maglia anche uscendo fuori dalla popolazione).

Ma è ben evidente che, se una molecola fuoriesce dal sistema (e dal connesso campo gravitazionale) essa non può subire alcuna modifica del suo stato energetico ed anche la sua variazione di posizione è soggetta a condizioni limitative espresse dal principio di inerzia. La variabilità mostrata è quindi effetto di scambio mentre le probabilità sono necessariamente desunte dalla frequenza degli stati molecolari nell’ambito del sistema complessivo. La condizione di partenza è quindi tipicamente di interdipendenza statistica, mentre Boltzmann ipotizza, al contrario, che la condizione sia di indipendenza statistica delle probabilità degli stati. Si tratta di un errore grave ai fini dello svolgimento della successiva trattazione, non accettabile neanche in via di approssimazione, giacché le due condizioni sono, ai fini di determinati, importanti sviluppi, diametralmente opposte. E’ già ben evidente, infatti, che in condizioni di interdipendenza statistica il sistema può assumere una sola configurazione, in quanto la modifica della configurazione comporta la variazione della frequenza e quindi della probabilità degli stati di posizione, il che implica la possibilità di variazione autonoma, non di scambio, di tali stati, quindi una condizione di indipendenza statistica degli stati.

  È bene sottolineare che la condizione di interdipendenza statistica degli stati non implica alcuna dipendenza funzionale fra di essi ma semplicemente il fatto che la probabilità di ottenere un dato stato scegliendo a caso un componente del sistema è data della frequenza con cui questo stato appare nel sistema complessivo. I vari stati vanno però considerati come entità assolutamente indipendenti e di comparsa assolutamente casuale, allo stesso modo come le frequenze dei colori di maglia dei componenti della popolazione nell’esempio citato di interdipendenza statistica non possono mutare, ma ciò non toglie che la prima costituzione delle frequenze dei colori possa essere una scelta assolutamente libera da vincoli, quindi casuale.

 Consideriamo adesso un problema che è connesso alle suesposte considerazioni. Lo stato macroscopico può essere considerato come composto di n eventi indipendenti, cioè di n successive estrazioni. La probabilità può quindi essere calcolata come il prodotto delle probabilità dei singoli eventi. E’ legittima questa procedura di calcolare la probabilità dell’evento complesso? Generalmente parlando, non lo è. Poiché l’estrazione è eseguita da un insieme finito, esiste una interdipendenza indiretta o da “container” delle successive estrazioni, cosicché l’ipotesi della loro indipendenza non può ritenersi verificata. Poiché tutti gli elementi vengono estratti dallo stesso insieme finito, ogni estrazione modifica la distribuzione degli elementi rimanenti e quindi il livello probabilistico delle successive estrazioni.

Ricordiamo che la probabilità di un evento complessivo costituito da due elementi semplici è moltiplicativa (cioè ottenibile dal prodotto delle due probabilità elementari) quando i due elementi hanno campi di variabilità completamente separati. In tal modo il campo totale, in cui la probabilità dell’evento complesso deve essere calcolato cresce in modo moltiplicativo (il numero di possibili eventi combinatori, cioè la dimensione del campo di variabilità dell’evento complesso si ottiene infatti moltiplicando tutti i punti dell’uno per tutti i punti dell’altro e sommando). Essa diviene invece additiva (ossia ottenibile per somma delle probabilità elementari, quando i due eventi si realizzano nello stesso campo, cosicché l’accadenza dell’uno riduce il campo di variabilità dell’altro.

Nel nostro caso, l’occorrenza di un certo numero di eventi riduce il campo di variabilità degli altri al fine di soddisfare non solo la relazione (1) ma anche per ottenere una struttura di frequenze eguale a quella delle probabilità, che impone ulteriori vincoli alla classe delle frequenze individuali. Cionondimeno in statistica si ritiene che, quando il numero di elementi estratti è molto piccolo in confronto al numero totale di elementi della popolazione, la modifica connessa a quest’ultima considerazione possa essere ignorata e la estrazione è considerata come avvenire in una popolazione infinita o universo (o può stabilirsi che, dopo ogni estrazione, l’elemento venga rimesso nella popolazione cosicché il suo campo di variabilità non venga influenzato dalla estrazione). In questo modo, l’intero campo di possibilità offerto dalla popolazione è aperto ad ogni elemento estratto e, in termini aprioristici, il processo effettivamente si svolge come se non vi fossero limiti nella dimensione del campo

La probabilità dell’evento complesso può allora essere valutata come prodotto delle probabilità dei singoli eventi elementari in quanto le modificazioni indotte nella popolazione dalla estrazione possono, in questi casi, essere ignorate. Tuttavia, l’aumento moltiplicativo delle dimensioni del campo di variabilità che è implicito nel calcolare la probabilità totale tramite il prodotto delle probabilità elementari, non può essere ignorato. Infatti il numero di combinazioni possibili non è rappresentato dalle combinazioni ottenibili se a ogni estrazione corrispondesse un differente campo di variabilità laddove ad ogni estrazione corrisponde lo stesso campo di variabilità.

Occorre quindi, in ogni caso, apportare al prodotto delle probabilità una correzione che tenga conto di questa necessità di “normalizzazione” del campo di variabilità che si aggiunge alla necessità di normalizzazione del campo delle probabilità, espresso dalla (1).

Assumendo un campione di dimensione n, si avranno np_k componenti con probabilità p_k e quindi, moltiplicando le probabilità di tutti gli elementi estratti si otterrebbe, come valore della probabilità complessiva:

P =∏(p_k)^npk                     (2)

Cioè un numero tendente rapidamente a zero con la dimensione del campione.

Tale risultato è privo di senso e riflette l’ampliamento esponenziale delle possibilità che si verifica per effetto della considerazione di campi di variabilità separati per ogni componente estratto con la conseguente rapidissima tendenza a zero della quota rappresentata dall’evento realizzato, cioè della sua probabilità. Va quindi eliminato l’aumento dimensionale del campo connesso alla presenza del coefficiente n nell’esponente della (2) e ciò è evidentemente molto facile, basta cassarlo.

Con queste premesse, ed effettuata l’operazione di normalizzazione del campo di variabilità, la probabilità del fenomeno complesso può essere ritenuta coincidere con il prodotto delle probabilità dei fenomeni elementari, ma ad ogni modo, per tener conto delle ipotesi semplificative che permettono tale affermazione, sopratutto del riferimento a campioni estratti da un universo piuttosto che da una popolazione finita, essa viene chiamata “verosimiglianza” e indicata generalmente con la lettera L, iniziale del termine anglosassone “likelihood”.

La verosimiglianza dello stato macroscopico sarà quindi espressa da:

L = ∏p_k)^pk                                (3)

Vi è però un elemento di ambiguità che l’introduzione della verosimiglianza mantiene: esso è costituito dal fatto che il numero di parametri a cui è assegnata la densità di probabilità non è necessariamente costante, ma può essere addirittura una funzione della dimensione del campione.

Per conseguenza, pur avendo eliminato l’elemento di ambiguità connesso all’esponente n della (2) il prodotto delle probabilità può tendere rapidamente a zero ed essere quindi privo di significato per l’aumentare del numero dei parametri i per ciascuno dei quali va determinato il livello di probabilità. Si dice che esiste una ambiguità connessa alla variabilità di scala del parametro a cui viene assegnata la densità di probabilità.

La normalizzazione realizzata dividendo l’esponente della (2) per n non è quindi completa, fintanto che il numero dei fattori al secondo membro della (3) è soggetto ad una variabilità di scala connessa alla variabilità del numero dei parametri o dei valori del parametro per i quali è richiesta la determinazione probabilistica.

La variabilità di scala implica che data una certa distanza individuata da un segmento di una retta, essa può essere espressa in modi diversi, intendendosi come tali diversi numeri di punti intermedi cui diamo importanza significativa. Ciò può accadere anche se consideriamo una infinità di punti di un segmento, cioè una condizione di continuità perché è possibile considerare infinità di punti di diverso ordine nell’ambito dello stesso segmento.

Il problema della eliminazione della variabilità di scala è un altro di quei problemi che mostrano quanto difficile sia la comprensione del significato e della generalità di certi risultati. Esso è stato infatti risolto da Bernoulli intorno al 1700 nell’ambito della dimostrazione della convergenza della binomiale alla gaussiana ridotta [2] ed il metodo adottato è stato poi applicato alla dimostrazione del teorema limite centrale del calcolo delle probabilità [3], nonché di altri importanti teoremi, ma senza che alcuno rilevasse la generalità di tale soluzione, così che il risultato generale è stato ricercato per secoli e ritrovato recentemente da Jaynes [6] riprendendo un’idea di Jeffrey [7], nell’ambito di un problema similare ed infine da me [8], in modo del tutto autonomo nell’ambito di un diverso problema.

Nel paragrafo che segue si riporta la elegante dimostrazione di Bernoulli, che commenteremo ove opportuno al fine di mostrare attraverso di essa il significato dell’operazione di normalizzazione ivi condotta e come dovrebbe essere facile, almeno intuitivamente, dedurne l’estensione al calcolo differenziale.

Consideriamo una variabile statistica distribuita secondo lo schema di Bernoulli

dove p e q sono le probabilità di accadenza (1) e di non accadenza (0) di un evento. Come è noto, la somma di n variabili statistiche distribuite secondo lo schema di Bernoulli può essere associata al polinomio:

 (pt + q)ⁿ       (5)

il cui termine generale dello sviluppo è dato dall’espressione di Newton:

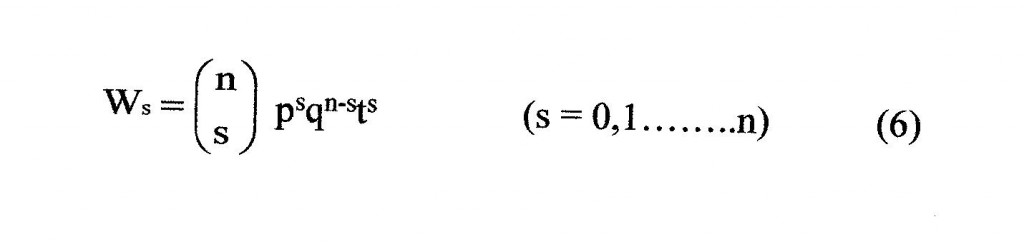cui corrisponde la variabile statistica:

ogni valore

relativo ad un valore di s, esprime la frequenza di s accadenze su n eventi indipendenti, ciascuno distribuito secondo lo schema di Bernoulli (4). La distribuzione di frequenza della variabile statistica (7) è detta distribuzione binomiale. E’ facile calcolarne la media e la varianza. Si ha infatti per la distribuzione elementare (4):

               media = m = (1xp+0xp)/(p+q) = p(p+q) = p

              varianza = σ²= (1-p)²p + (0-p)²q = pq                                            (8)

Ne segue che per la variabile (7) somma di n variabili elementari (4) si ha:

            m = np                           σ²= npq                 (9)

Come si vede, quindi, l’intervallo (0,1) della variabile originaria, definito da due soli punti, ha assunto nella variabile somma n+1 punti significativi, cioè ha assunto una variabilità di scala. E’ facile vedere che ciò determina una tendenza a zero di tutte le probabilità al crescere del numero di variabili statistiche somma, cioè di n, che cioè l’espressione generica della probabilità tende a zero con il crescere di n ed assume quindi una ambiguità connessa all’esistenza di una variabilità di scala. Dimostriamolo per il massimo valore della frequenza, valore che si ha in corrispondenza di un valore i della variabile s per cui si ha:

che comporta:

                                                   i > pn-q                                   (11)

Per grandi valori di n si può allora porre i = pn e pertanto W_i diviene:

Applicando la formula di De Moivre Stirling, valida per grandi valori di n:

si ha, sostituendo in (12):

e quindi, per n tendente all’infinito.

Se però sostituiamo ai valori della variabile statistica di partenza (4) gli scarti rispetto alla media rapportati allo scarto quadratico medio totale (i cosiddetti scarti ridotti) se cioè partiamo da variabili statistiche del tipo:

la variabile statistica X⁽ⁿ⁾ somma di n di tali variabili, al tendere di n all’infinito tende ad una forma limite la cui distribuzione di frequenza è data dalla formula:

detta “Gaussiana ridotta”.

Basta, per dimostrare questa affermazione, applicare l’inversa del primo teorema limite del calcolo delle probabilità e dimostrare che la funzione generatrice della variabile statistica somma X⁽ⁿ⁾ tende alla funzione generatrice della gaussiana ridotta. Ci risparmiamo il dettaglio di questa dimostrazione, contenuta in tutti i testi di statistica ed in particolare nel mio testo citato in bibliografia, cap. II, pagg, 25 e 26 [4].

Ciò che a noi interessa è che il passaggio agli scarti ridotti, cioè a variabili anche dette normalizzate, che viene svolto anche nella dimostrazione di altri importantissimi teoremi, quale il teorema limite centrale del calcolo delle probabilità, può essere espresso in termini differenziali come sostituzione della variazione elementare d con la variazione d/, cui corrisponde, a livello integrale, il passaggio ai logaritmi.

Come ho avuto modo di accennare, tale conclusione è stata ritrovata da Jaynes, assai recentemente, attraverso la cosiddetta “teoria della marginalizzazione” [6], nell’ambito di una ricerca volta ad eliminare l’ambiguità connessa alla variabilità di scala del parametro cui viene assegnata la uniforme densità di probabilità nel teorema di Bayes e Laplace. Lo stesso risultato è stato da me ottenuto in un altro contesto [8].

Dunque la variabilità di scala di un parametro  viene eliminata sostituendo le variazioni differenziali del parametro, d, con il rapporto d/, il che implica, a livello integrale, l’assunzione di una scala logaritmica. La verosimiglianza, nella sua forma logaritmica, diviene:

cioè la verosimiglianza normalizzata coincide (trascurando il segno) con l’entropia statistica. Per quanto abbiamo più sopra detto, essa è quindi libera dalle ambiguità connesse alla variabilità di scala del parametro cui è assegnata la densità di probabilità.

E’ opportuno che ci soffermi ancora sul concetto che la verosimiglianza normalizzata, o l’entropia, pur coincidendo con la probabilità dell’evento complesso quando questo costituisce un piccolo campione estraibile da una popolazione infinita, non può essere assolutamente con essa confusa quando ci si allontani da queste ipotesi estremamente restrittive assumendo eventi complessi la cui dimensione non sia più trascurabile nei confronti della popolazione o addirittura la esauriscano, per considerare quali sono i motivi per cui essa rimanga pur tuttavia, anche in queste condizioni un indice di estrema importanza.

L’entropia, come prodotto delle frequenze normalizzate, è in rapporto univoco con la struttura distribuzionale della popolazione o del campione e rappresenta perciò un indice distribuzionale, una misura della variabilità.

Come è ben noto agli studiosi di statistica, sono stati proposti numerosi indici che possano rappresentare sinteticamente una distribuzione di frequenza. Evidentemente, vista la ovvia impossibilità teorica di sintetizzare in un solo indice informazioni così numerose e complesse quali sono racchiuse in una distribuzione di frequenza, la scelta dell’indice assume degli aspetti soggettivi, risultando un indice più adatto ad un problema piuttosto che ad un altro. Cionondimeno un indice ha avuto un successo particolare in virtù del fatto che si inquadra come componente in un quadro matematico che permette l’analisi completa della variabilità. Mi riferisco alla varianza o momento del secondo ordine, che rappresenta il secondo termine dello sviluppo in serie di una funzione, detta funzione caratteristica, che può essere trasformata, attraverso il teorema di inversione di Fourier, nella funzione distribuzionale [5].

Quindi, seppure non è possibile trasferire l’intera quantità di informazione contenuta in una funzione distribuzionale in un solo indice, è possibile trasferirla in una successione di indici, o momenti, che rappresentano lo sviluppo in serie della funzione caratteristica e fra i quali il momento del secondo ordine occupa un posto di particolare importanza, visto che generalmente il resto dello sviluppo in serie tende rapidamente a zero.

E’ possibile quindi apprezzare il significato dell’entropia mediante il raffronto fra le variazioni dell’entropia e le variazioni del momento del secondo ordine.

E’ innanzi tutto evidente che, poiché le probabilità sono valori frazionari, l’entropia diminuisce all’aumentare del numero dei fattori, cioè del numero delle classi di frequenza. Poiché parliamo di campi variazionali normalizzati, in cui cioè è eliminata la variabilità di scala, la riduzione del numero delle classi, e quindi l’aumento dell’entropia, riflette la reale riduzione degli elementi di variabilità o distinguibilità, ossia la diminuzione dell’ampiezza del campo di variabilità normalizzato e quindi della varianza. L’entropia è un indice distribuzionale che varia in modo inverso alla varianza, è cioè, con i termini di Gini, un indice di “concentrazione”.

Naturalmente, non ignoriamo che la varianza dà un peso crescente agli elementi della variabile statistica a seconda della differenza dei loro valori dalla media, laddove nell’entropia statistica il solo elemento considerato è la frequenza, quale che sia il valore dell’elemento. Quindi nell’entropia statistica la distinguibilità degli elementi è determinata dalla selezione apriori degli eventi elementari a cui è assegnata una densità di probabilità e a cui l’operazione di normalizzazione riporta. Nella varianza invece, la distinguibilità entra anche attraverso i valori della variabile statistica che entrano nel calcolo dell’indice e non solo nella determinazione delle classi di frequenza. Quindi nella varianza è possibile graduare la distinguibilità o differenziazione, laddove nell’entropia la distinguibilità ha solo due livelli: si e no. Quindi l’entropia statistica non è adeguata al trattamento di fenomeni in cui la variabile statistica (che esprime la distinguibilità) varia secondo una quantità numerabile, mentre è adeguata alla trattazione di fenomeni in cui la variabile statistica varia per attributi.

In ogni caso, l’entropia è influenzata dalla determinazione aprioristica degli elementi di distinguibilità che può essere, in una certa misura, arbitraria, come è mostrato dal famoso paradosso di Gibbs [9].

Gibbs mostrò che le conseguenze fisiche del mischiare due gas “quasi identici” sono essenzialmente le stesse del mischiare due gas identici. Tuttavia la variazione di entropia data dalla relazione di Boltzmann è grande per molecole distinguibili mentre è zero per molecole identiche. Malgrado siano passati più di cento anni da quando Gibbs formulò il suo paradosso, non è stata ancora trovata una spiegazione soddisfacente.

Alla luce della nostra analisi la sua soluzione è chiara. Assumendo un elemento di poca importanza ai fini della distinguibilità, come è implicito nei termini “quasi identici”, come elemento fondamentale di determinazione del campo di variabilità normalizzato gli si dà la massima importanza proprio per quanto riguarda la distinguibilità, così introducendo la possibilità di valutazioni erronee se l’entropia non è valutata in relazione al valore elementare di distinguibilità definito apriori.

In altre parole, l’entropia deve essere valutata in relazione al valore elementare di distinguibilità dato a una classe rispetto ad un’altra, valore che non entra nel calcolo dell’indice come invece avviene nella varianza.

Nella dimostrazione di Boltzmann della legge dell’ aumento dell’entropia statistica la scelta arbitraria di distinguibilità consiste nella dimensione della cella elementare.. Tale cella venne scelta in modo da contenere un gran numero di particelle, cosicché il numero dei modi con cui una configurazione può essere realizzata è dato da:

La sua espressione logaritmica è l’entropia coincidente (come ha mostrato Shannon utilizzando la formula di De Moivre Stirling e tenendo conto che N_k/N = p_k) con l’opposto della espressione (18). In essa N_kè il numero di particelle contenute nella cella k. Secondo Boltzmann, la configurazione più probabile è quella per la quale la eq. (19) diviene massima.

Ora, i fattori N_k! Esprimono le permutazioni degli elementi contenuti all’interno delle celle cosicché eq. (19) esprime le permutazioni residue fra le celle.

Evidentemente il valore dell’eq. (19) aumenta quando le particelle sono suddivide fra le celle (perché aumentano le permutazioni fra le celle) e diminuisce quando le particelle sono condensate nelle celle (perché aumentano le permutazioni nelle celle). Ma il valore dell’eq. 19, e quindi dell’entropia, aumenta anche se la dimensione delle celle decresce perché anche in questo caso le permutazioni fra le celle aumentano. Quindi l’entropia dipende dalla dimensione delle celle che cambia l’ elemento di distinguibilità. Da notare che le differenze in entropia fra le configurazioni diminuisce quando la dimensione delle celle diminuisce: se scegliamo una cella così piccola da contenere solo una particella, tutti i fattori N_k! dell’eq. (19) divengono unitari ed il numero di modi di combinazione dei microstati diviene N! quale che sia la configurazione!

Ritorniamo allora al problema da cui siamo partiti, vale a dire la determinazione della distribuzione delle frequenze degli r stati in cui ciascun elemento di un insieme può trovarsi in condizioni di interdipendenza statistica ed in particolare delle frequenze di posizionamento che individuano la forma del sistema, cioè la configurazione del sistema. Ricordiamo la conclusione cui siamo giunti che in condizioni di interdipendenza statistica può esistere una sola configurazione in quanto la modifica della configurazione implicherebbe la variazione delle frequenze degli stati di posizionamento che in una condizione di interdipendenza statistica di un sistema isolato non possono sussistere.

Con ciò ovviamente non abbiamo determinato quale sia questa configurazione, anche se sappiamo che è unica; ricordiamo però che la prima formazione della distribuzione di frequenza è un processo casuale.

Noi possiamo in tal caso applicare il principio di indifferenza di Laplace e la conseguente legge dei grandi numeri di Bernoulli. Essa stabilisce che in simili casi in cui non vi è alcuna ragione a priori per dare differenti probabilità agli stati elementari si deve assumere una condizione di eguale probabilità e ritenere che l’esistenza di una non uniformità distribuzionale sia equivalente all’esistenza di una causa agente,

Si può dimostrare che, quando le probabilità degli stati elementari sono eguali, il livello di entropia di tale distribuzione è superiore a quello ottenibile con qualsiasi altra distribuzione. Dimostriamolo per semplicità nei confronti della verosimiglianza.

La condizione di normalizzazione delle frequenze impone:

Il massimo della verosimiglianza richiede l’annullamento della derivata, cioè per Max(p_1*p_2*……)deve essere:

Ma essendo

si deve avere:

p₁ = p₂ = ….ecc                       (22)

Dunque, la configurazione di massima entropia non è la configurazione più probabile, ma l’unica possibile.

Ma allo stesso risultato si può giungere attraverso una diversa linea di ragionamento, senza necessità di passare dalla legge dei grandi numeri. Supponiamo che tutti i componenti del sistema abbiano lo stesso stato energetico, cioè lo stesso livello di energia cinetica.

Perché i differenti modi di combinazione diano luogo a configurazioni distinguibili vi devono essere differenze nella composizione delle celle in cui il sistema viene diviso. Ciò implica una variabilità della densità dei componenti e quindi differenziali dell’energia totale fra una cella e l’altra.

Quindi, una variabilità configurale può esistere solo sotto condizioni di disequilibrio [10], altrimenti le diverse combinazioni di celle son indistinguibili. Tuttavia, poiché le condizioni di disequilibrio tendono, per il postulato di Carnot, verso l’equilibrio e poiché queste condizioni di equilibrio non possono essere abbandonate, in definitiva sotto condizioni di equilibrio solo una configurazione macroscopica è possibile.

Conclusioni

L’ipotesi di Boltzmann è quella di equiprobabilità dei modi di combinazione degli stati per realizzare le configurazioni. Ma alle diverse configurazioni corrispondono diverse distribuzioni di frequenza degli stati e quindi diverse distribuzioni delle probabilità elementari. Poiché abbiamo visto che le distribuzioni asimmetriche delle probabilità elementari non sono possibili in assenza di una causa sistemica (secondo la locuzione di Prigogine esistono “vincoli di simmetria”), l’ipotesi di Boltzmann contraddice clamorosamente il principio di indifferenza di Bernoulli ed equivale ad ammettere che vi siano effetti senza cause.

Si tratta di un errore metodologico grave, che è stato possibile commettere e non rilevare dopo che era stato commesso, in virtù di una condizione di impossibilità ancora più grave cui sembrava condurre la sua negazione, quella della impossibilità della formazione dell’ordine nei sistemi isolati. Infatti, malgrado attraverso l’ipotesi di Boltzmann si debba considerare come macrostato più probabile quello ottenibile con il maggior numero di modi di combinazione che è quello di massima entropia, sussistono probabilità di passaggio per macrostati diversi, che possono determinare l’innesco di un meccanismo evolutivo (ipotesi ergodica), probabilità che seguendo lo schema di Bernoulli debbono invece escludersi.

Ma una contraddizione non è mai stata risolta da un’altra contraddizione: se, invece di cercare impossibili modo di formazione dell’ordine per via casuale, si fosse considerato che le conclusioni ottenute tramite lo schema di Bernoulli dimostrano la necessità dell’esistenza di un fattore sistemico nascosto, questo sarebbe stato alla lunga trovato, come ho avuto modo di mostrare in altri lavori [11]

Bibliografia

[1] – Jaynes E.T.:Where do we stand on maximum entropy? In “The maximum entropy Formalism” Levine & Tribus ed., MIT Press, 1978

[2] – Firrao S.: Controllo Statistico della Qualità, Politecnico di Milano, 1968, pag. 25

[3] – Ibidem, pag. 29

[4] – Ibidem pag. 25 e 26

[5] – Ibidem, pag 18

[6] – Jaynes .T.: Foundations of Probability Theory, Statistical Inference and Statistical Theories of Sciences, W.L. Harper and C. A. Hooker eds, D. Reidel Publishing Co. Dordrecht, Holland, 1976

[7] – Jeffreys H.:Theory of Probability, Oxford University Press, 1948

[8] – Firrao S.:Sui fondamenti della termodinamica, in Studi sui sistemi complessi, Lulu, cap. 2

[9] – Gibbs J.W. : Principles of Statistical Mechanics, Yale University Press, New Haven, 1948

[10] – Prigogine I., Nicolis G.: Self-Organization in Non-equilibrium Systems, Wiley, New York, 1977

[11] – Firrao S.: Development of Oscillatory Processes in Isolated High Energy Systems, Cibernetica, XXXI, 4, 1988

.