1-Richiamo di alcuni fondamentali proposizioni di analisi infinitesimale.
L’integrale indefinito di una funzione f(x) è determinato a meno di una costante C, cioè:
∫f(x)dx = F(x) + C (1.1)
giacché ovviamente la derivata di una costante è zero.
L’ integrale definito nell’intervallo di integrazione (a,b), cioè la differenza della funzione integrale fra i punti finale e iniziale, è allora
∫(a,b)f(x)dx = F(b) + C – F(a) – C = F(b) – F(a) (1.2)
dove la eventuale componente costante scompare. Ovviamente, tale differenza può assumere un solo valore perché una sola è la variabile da cui la funzione dipende, si dice che il differenziale dy = f(x)dx è un differenziale esatto.
Se però noi partiamo dall’integrale definito in (a,b) cioè dalla (1.2), non possiamo dire che, poiché il differenziale è esatto la f(x) sia funzione solo della x perché la funzione potrebbe dipendere anche da un’altra variabile che è assente o si mantiene a valore costante nella nostra condizione sperimentale, ma potrebbe invece esistere e variare in un’ altra condizione sperimentale.
Il risultato può essere esteso alle funzioni di più variabili; ai nostri fini interessa però il caso di una funzione di due variabili. Il fatto che il suo differenziale sia esatto, cioè che l’integrale definito sia determinato dai valori assunti dalle due variabili negli estremi dell’intervallo di integrazione, non esclude l’esistenza di altre variabili indipendenti che siano assenti o si mantengano costanti nelle nostre condizioni sperimentali.
Vale quindi la considerazione che, se il differenziale di una funzione di due variabili non è esatto, deve necessariamente esistere una causa della sua variabilità, A differenza però di quanto detto per la funzione di una sola variabile, in questo caso la causa può non essere costituita da una terza variabile ignota da cui dipende la funzione, ma dal rapporto fra le due variabili note che può variare nelle diverse condizioni sperimentali.
Agganciandoci al lavoro di Pfaff [1] sulle equazioni differenziali possiamo affermare che in questi casi, che definiscono la cosiddetta “variabilità di scala”, è sempre possibile trovare un fattore di integrazione che permetta l’integrazione del differenziale (cioè lo renda esatto). É evidente allora che se proviamo ad integrare una funzione che riteniamo dipendere da due sole variabili indipendenti e la integrazione risulta impossibile perché il differenziale risulta inesatto, dobbiamo prima verificare se tale inesattezza è dovuta ad una variabilità di scala ricercando un possibile fattore di integrazione. Se però risulta impossibile trovare un fattore di integrazione, la funzione non può variare in funzione solo di due variabili indipendenti, essa necessariamente varia in funzione di almeno tre variabili indipendenti.
Dimostriamo allora che, in un caso particolare in cui la funzione di due variabili indipendenti ha un differenziale inesatto per la presenza di una variabilità di scala, tale variabilità viene eliminata dalla moltiplicazione della funzione per un fattore di integrazione.
2 – Eliminazione della variabilità di scala della funzione prodotto.
Sia z una funzione del prodotto yx, a sua volta ovviamente funzione delle due variabili indipendenti y ed x. Consideriamo quindi, nel piano di coordinate y ed x un intervallo definito dai valori assunti dalle coordinate ai suoi estremi e, in tale intervallo, tutte le traiettorie che possono unirne i punti iniziale e finale. Sia ds la componente elementare della traiettoria generica s. Possiamo scrivere:
dz=(dz/dyx) d(yx)/ds ds (2.1)
e tale differenziale non può essere esatto, ossia il suo integrale non può essere costante passando da una traiettoria all’altra perché già l’integrale di ds, che esprime la lunghezza della traiettoria, è variabile da una traiettoria all’altra.
Quindi, non è sufficiente che la funzione z dipenda solo da due variabili perché il suo differenziale sia esatto: occorre che la funzione y=f(x) che identifica la traiettoria nel piano di coordinate y ed x, venga definita univocamente, cioè sia eliminata la variabilità di scala.
Dimostriamo che la divisione del differenziale dz per il prodotto yx elimina la variabilità di scala, ossia che 1/yx costituisce un fattore di integrazione che rende esatto il differenziale dz se la sua inesattezza dipende solo dalla variabilità di scala del prodotto yx.
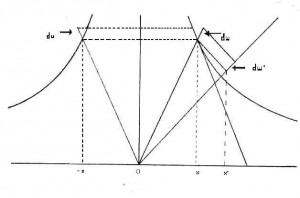
In ogni punto del piano di coordinate y ed x vi sono due direzioni che identificano variabili che non possono essere direttamente interdipendenti. Queste direzioni sono: la direzione w identificata dalla linea che congiunge il punto con l’origine degli assi, in cui può variare il prodotto yx ma non il rapporto y/x e la direzione u, identificata dall’iperbole equilatera che passa attraverso il punto in cui può variare il rapporto y/x ma non il prodotto yx.
Conseguentemente, in ogni punto della traiettoria il differenziale ds può essere diviso nella componente d(yx) in direzione w e nella componente d(y/x) in direzione u. Poiché z è funzione del prodotto yx e quest’ultimo può variare solo nella direzione w, possiamo così riscrivere la (2.!)
dz = dz/d(yx) d(yx)/dw dw (2.2)
Proiettiamo dunque ds sulle due direzioni w e u (vedi figura) così ottenendo i segmenti dw e du cui corrispondono i differenziali d(yx) e d(y/x). In figura abbiamo anche tracciato l’asse di simmetria del primo quadrante del piano di coordinate y ed x, ossia l’asse inclinato a 45 gradi passante per l’origine degli assi e che abbiamo indicato con il simbolo w’. Proiettiamo quindi il punto esaminato sull’asse di simmetria. Il triangolo definito dai segmenti w e w’ ed il triangolo definito dai segmenti w+dw e w’+dw’ sono simili e noi possiamo quindi scrivere:
dw/w = dw’/w’
Ciò si verifica quale che sia la congiungente con l’origine degli assi e quindi, sostituendo w con la sua espressione in termini di prodotto yx:
dw/yx = C (2.3)
dove C è una costante. Vediamo cosa ciò comporta. Come abbiamo già detto, ogni elemento di traiettoria ds può essere considerato come composto da uno spostamento lungo la congiungente il punto iniziale con l’origine degli assi, in cui varia il prodotto yx e uno spostamento lungo l’iperbole, in cui il prodotto yx non varia, ma varia il punto finale dell’elemento che è poi quello iniziale del successivo elemento di traiettoria che per conseguenza giace su una diversa congiungente con l’origine degli assi in cui la progressione del prodotto yx è diversa. Il differenziale dw, componente elementare della traiettoria nella variabile yx varierà dunque in dipendenza della lunghezza dello spostamento lungo l’iperbole da cui dipende il suo spostamento su una diversa semiretta che inizi dall’origine degli assi. Come abbiamo mostrato in figura, tutti i segmenti che esprimono la variazione dw nei vari assi hanno la stessa proiezione sull’asse di simmetria cui corrisponde, come mostrato nella (2.3) la divisione del differenziale dw per il prodotto yx. La variabilità di scala del differenziale dw che, come si vede, dipende dalla scelta iniziale del rapporto y/x di ogni elemento di traiettoria, da cui dipende la determinazione della congiungente con l’origine degli assi, è stata dunque eliminata dividendo per yx. Quindi, nell’espressione del differenziale dz/yx:
dz/yx =dz/d(yx) d(yx)/ds ds/yx (2.4)
il solo elemento che può variare con è dz/d(yx), ossia la inesattezza di dz/yx può essere dovuta esclusivamente alla variabilità di dz a parità di d(yx), quindi ad una terza variabile.
3- I dati sperimentali e la loro interpretazione.
Consideriamo un sistema gassoso che riceve calore dall’esterno ed esegue lavoro sull’esterno. Per la prima legge della termodinamica possiamo scrivere:
dq = dU + dW (3.1)
dove dq è la quantità elementare di calore assorbita dall’esterno, dU l’aumento elementare dell’energia interna, dW la quantità elementare di lavoro eseguito sull’esterno e dove i due termini al secondo membro sono funzioni delle variabili di stato p, pressione e v, volume.
I risultati delle prime trasformazioni termodinamiche progettate per trasformare in lavoro le forze sviluppate da un disequilibrio termico mostrarono che il differenziale dq relativo ad una variazione elementare delle variabili di stato non è integrabile, non costituisce cioè un differenziale esatto laddove, dividendo entrambi i membri della (3.1) per la temperatura T, almeno in un certo tipo di trasformazioni (le reversibili), il differenziale dq/T diviene esatto.
Vennero dunque introdotti due tipi fondamentali di trasformazioni, le irreversibili e le reversibili e si osservò che il rapporto dq/T fra la quantità elementare di calore assorbito e la temperatura è un differenziale inesatto nelle variabili che definiscono lo stato nelle trasformazioni irreversibili, mentre è un differenziale esatto nel caso delle trasformazioni reversibili. Inoltre, a parità di stato, il rapporto dq/T ha un valore minore nelle trasformazioni irreversibili. Ciò può essere espresso per mezzo della seguente formula:
(dq/T)i < (dq/T)r (3.2)
dove l’introduzione dei due tipi di trasformazioni – irreversibili e reversibili – è rappresentato dagli indici sottoscritti che accompagnano i differenziali e dove inoltre il differenziale sulla sinistra è inesatto mentre quello sulla destra è esatto.
Consideriamo adesso la spiegazione che può essere data dei risultati sperimentali ottenuti partendo dalla constatazione che la quantità dq non è integrabile nei confronti delle variabili di stato mentre lo è la quantità dq/T, almeno nell’ambito delle trasformazioni reversibili.
La spiegazione è molto semplice dopo quanto abbiamo fin qui esposto: la non integrabilità del differenziale dq in funzione di due variabili, cioè la sua variabilità, implica semplicemente che sul fenomeno agisce una terza variabile. L’affermazione che una variabilità presuppone una variabile può sembrare lapalissiana; tuttavia può accadere che la terza variabile non sia una variabile indipendente che agisca direttamente sulla funzione, ma giaccia nel rapporto dimensionale fra le altre due variabili, che la variabilità sia cioè una variabilità di scala. In questi casi però il differenziale può essere sempre reso esatto mediante la moltiplicazione per un fattore di integrazione; per conseguenza, quando non esiste un fattore di integrazione che renda integrabile la funzione è giocoforza riconoscere che sul fenomeno agisce una terza variabile.
Nel caso di specie quindi, sussistendo un fattore di integrazione rappresentato dal rapporto 1/T, la variabilità del differenziale dq è una variabilità di scala, giace cioè nel rapporto dimensionale fra le due variabili di stato pressione e volume. Prendendo infatti in considerazione l’equazione di stato dei gas perfetti:
pv = RT (3.3)
dove R è la costante dei gas e T la temperatura, possiamo scrivere:
dq/T = Rdq/pv (3.4)
e tenendo presente la (2.4) possiamo quindi dire che dq/T è l’espressione normalizzata, del differenziale dq, in cui cioè sono eliminati gli effetti della variabilità del rapporto fra le due variabili indipendenti, detta variabilità di scala.
Per conseguenza la diversità dei risultati dell’integrale di dq/T, pur a parità dei valori assunti dalle due variabili di stato note (p e v) agli estremi dell’intervallo di integrazione espressa dalla (3.2), implica necessariamente l’esistenza nelle trasformazioni irreversibili di una terza variabile di stato che è assente o si mantiene costante nelle trasformazioni reversibili.
Alla luce della teoria cinetica dei gas è abbastanza ovvio legare la terza variabile di stato alla distribuzione interna dei microstati. E’ infatti verosimile che la distribuzione interna dei microstati influenzi l’energia e la frequenza delle molecole dirette verso le resistenze esterne e per conseguenza il lavoro fatto su di esse. L’integrale di dq/T, raggiunge il suo massimo nelle trasformazioni reversibili per effetto di una certa distribuzione dei microstati che implica un equilibrio termico interno ossia l’assenza di disequilibri interni che riducano la frequenza delle molecole dirette verso le resistenze esterne. Le trasformazioni irreversibili, invece, involvono disequilibri interni che riducono il numero di molecole dirette verso le resistenze esterne e quindi il lavoro che può essere fatto su tali resistenze. Ciò giustifica il segno < nell’equazione (1.5).
Se i disequilibri interni fossero costanti nel corso delle trasformazioni, per tutte le trasformazioni aventi un determinato valore dei disequilibri, il differenziale dq/T sarebbe un differenziale esatto, quantunque minore che nella condizione di equilibrio; ma per il postulato di Carnot e Clausius, secondo cui il calore fluisce dalle zone a più alta temperatura verso quelle a più bassa temperatura, il disequilibrio interno si riduce gradualmente nel corso della trasformazione. La velocità con cui il disequilibrio si riduce può essere diversa da una traiettoria all’altra pur con lo stesso valore iniziale dei disequilibri ed è così causa di inesattezza del differenziale.
La terza variabile potrebbe essere perciò identificata nell’entropia statistica di Boltzmann [7] che costituisce un indice che misura il livello di omogeneizzazione della condizione di stato nel sistema e che riferendoci, come si fa in statistica, al diagramma distribuzionale delle frequenze, sarebbe un indice di “concentrazione” della distribuzione di frequenza dei microstati.
4 – L’interpretazione di Clausius.
Secondo Clausius invece, l’esattezza del differenziale dq/T nelle trasformazioni reversibili implica che il suo integrale sia dipendente unicamente dalle due variabili di stato p e v con ciò escludendo che possa esistere una terza variabile di stato non identificata che agisca in termini differenziali nelle trasformazioni irreversibili.
Si tratta di un errore perché contraddice un risultato elementare del calcolo differenziale che è anche intuitivo; è evidente infatti che, nell’ipotesi di assenza o di costanza di una terza variabile, essa non potrebbe influenzare il differenziale della funzione dovuto alla variazione delle altre due variabili di stato, ma potrebbe farlo in altre condizioni sperimentali in cui sia presente e variabile da una trasformazione all’altra e magari anche nell’ambito di una stessa trasformazione.
Se poi, con gli stessi valori delle variabili di stato che definiscono l’intervallo di integrazione e con la sicura assenza di una variabilità di scala (eliminata con la divisione per T), come avviene nelle trasformazioni irreversibili, la funzione risulta non integrabile, allora la presenza di una terza variabile di stato costituisce una certezza matematica. La negazione di quest affermazione costituirebbe anzi la negazione di un principio fondamentale del metodo scientifico secondo cui se la ripetizione di un esperimento con gli stessi precisi valori delle variabili dà luogo ad un risultato diverso, allora deve sussistere una ulteriore variabile che nel precedente esperimento non agiva.
Partendo dunque dalla erronea idea che l’integrale del differenziale dq/T sia funzione delle sole variabili p, pressione e v, volume, Clausius ne deduce che esso dovrebbe pertanto sussistere, con lo stesso valore, anche nei corrispondenti stati delle trasformazioni irreversibili (ossia stati con gli stessi valori di p e v). Ma, pur a parità dei valori delle variabili di stato, il rapporto dq/T è nelle trasformazioni irreversibili più basso del valore che compare nelle trasformazioni reversibili. Al fine di superare questa difficoltà Clausius suppose l’esistenza di una funzione dipendente unicamente dalle due variabili di stato, quindi a differenziale esatto, chiamata entropia, generalmente indicata con il simbolo S, che costituirebbe il supporto interno del lavoro esterno, la capacità produttiva. Questa capacità potrebbe essere completamente utilizzata nelle trasformazioni reversibili dando luogo all’integrale di (dq/T)r che potrebbe pertanto essere assunto anche come misura di questa capacità e sarebbe invece solo parzialmente utilizzata nelle trasformazioni irreversibili, dando luogo all’integrale di (dq/T)i che potrebbe quindi essere assunto a misura dell’entropia utilizzata in queste trasformazioni, ma sussisterebbe comunque anche la parte inutilizzata, chiamata “produzione interna di entropia” e indicata con il simbolo dSi in misura tale che sommata alla parte utilizzata ricostituisca il valore dell’entropia delle trasformazioni reversibili, così salvando la affermazione che l’entropia è funzione unicamente delle due variabili di stato p e v. Si avrebbe cioè:
(dq/T)i + dSi = (dq/T)r (4.1)
Clausius applicò cioè un metodo simile a quello adottato da Newton nella trattazione della interazione gravitazionale di due gravi. Dovendo soddisfare la legge di conservazione dell’energia in fase di allontanamento dei due gravi, in cui l’energia cinetica andava diminuendo, introdusse una forma invisibile di energia che definì potenziale e tale artificio permise la sussistenza della teoria che, d’altra parte, funzionava perfettamente in termini di risultati sperimentali. Come è noto, la teoria fu corretta da Einstein [6] che spiegò trattarsi di trasformazione di energia in massa e che la differenza nei risultati ottenibili con le due teorie era inavvertibile per effetto della enorme dimensione del rapporto di trasformazione energia-massa.
Ma l’introduzione della energia potenziale di Newton fu dovuta a quella che sembrava una necessità inderogabile, quella di soddisfare la legge di conservazione dell’energia, così non contraddicendo il fondamentale principio epistemologico “entia non sunt multiplicanda preater necessitatem” mentre la necessità che portò Clausius all’ introduzione dell’entropia e della produzione interna di entropia non sussisteva del tutto, ma era frutto di un errore analitico.
Anche la teoria di Clausius fu accettata perché sembrava che funzionasse perfettamente ai fini pratici in cui la variazione della produzione interna di entropia di Clausius svolgeva in fondo la stessa funzione della variazione dell’entropia statistica talché lo stesso Boltzmann [7] ne sostenne l’equivalenza.
Tuttavia, secondo la teoria di Clausius, in ogni stato caratterizzato da un certo valore delle variabili di stato p e v, l’entropia dovrebbe essere presente in corrispondenza univoca, anche in presenza di un valore minore del rapporto dq/T mostrato dalla trasformazione irreversibile rispetto al valore mostrato nello stesso stato della trasformazione reversibile, in quanto la parte residua sarebbe coperta dalla parte “invisibile” costituita dalla produzione interna di entropia. La presenza di una parte “invisibile” dell’entropia statistica che è un indice di omogeneizzazione, cui corrisponde quindi una forma della struttura delle interazioni interne al sistema, è un concetto impossibile da accettare nella costruzione di Boltzmann anche se lo stesso Boltzmann non aveva colto questo aspetto. E’ infatti ovvio che una grande varietà di disomogeneità distribuzionali dei microstati può sussistere in corrispondenza degli stessi valori delle variabili p e v e che per conseguenza nella costruzione di Boltzmann l’entropia è una variabile idi stato indipendente, mentre nella costruzione di Clausius è una variabile dipendente dalle variabili p e v da lui considerate le uniche variabili di stato.
In realtà però nella maggior parte dei casi pratici il risultato di un basso valore dell’indice di omogeneizzazione (entropia statistica) è quello di ridurre l’assorbimento di calore e la produzione di lavoro a fronte di una capacità teorica che il sistema avrebbe con un alto indice di omogeneizzazione, cioè lo stesso effetto di un alto valore della produzione interna dell’entropia termodinamica di Clausius. A differenza però di quanto accaduto per l’energia potenziale di Newton, in cui l’errore concettuale. operando su elementi infinitesimali, non poteva avere conseguenze sui risultati pratici, nel caso della teoria di Clausius possono mettersi in evidenza condizioni in cui la teoria può essere falsificata non solo sul piano logico (come abbiamo già fatto per quanto riguarda il significato dell’esattezza e della inesattezza del differenziale della quantità normalizzata di calore assorbito) ma anche dei risultati sperimentali, di alcuni dei quali riferiremo più avanti.
5- La formulazione di Clausius della seconda legge della termodinamica.
Desideriamo infatti mostrare con precedenza quali errori possono farsi nella impostazione di una teoria quando l’obiettivo è solo quello di giustificare i risultati ottenuti dall’esperienza non tenendo conto che gli stessi risultati possono essere giustificati da una infinità di teorie mentre una sola è quella che più si avvicina alla realtà o meglio che ha la massima ampiezza di validità euristica.
Esaminiamo a tal fine il ragionamento che ha portato Clausius alla sua enunciazione della seconda legge della termodinamica partendo dalla sua relazione tra le trasformazioni irreversibili e quelle reversibili:
(dq/T)i + dSi = (dq/T)r (4.1)
con il significato dei simboli che ormai conosciamo e dove i differenziali sono riferiti ad una variazione elementare del tempo.
Clausius considera quindi una trasformazione irreversibile di un sistema isolato e, poiché nei sistemi isolati non sono possibili scambi con il mondo esterno, ritiene che il rapporto (dq/T)i debba considerarsi identicamente nullo. Sostituendo per conseguenza zero a (dq/T)i nella (4.1) si ottiene:
(dq/T)r = dSi ≥ 0 (4.2)
e l’entropia quindi aumenterebbe per effetto della positività della produzione interna di entropia dSi.In ciò consiste la formulazione della seconda legge della termodinamica secondo Clausius.
Tale formulazione presenta difetti logici che a me sembrano assai evidenti. Infatti, in un sistema che, a parte eventuali vincoli di contenimento, sia per altri versi isolato, non può esistere alcuna trasformazione perché mancherebbe il motore del processo costituito dall’afflusso di calore dall’esterno. In particolare non può esistere alcuna trasformazione irreversibile, a meno che un disequilibrio interno sia la conseguenza temporanea di un calore assorbito dall’esterno prima che il sistema divenisse isolato. Tale quantità di calore è dunque parte integrante della trasformazione perché è all’origine della sua stessa esistenza e quindi delle modifiche in atto anche dopo l’inizio dell’isolamento.
Se dunque si vuole considerare quella parte della trasformazione che si manifesta dopo l’isolamento del sistema occorre ricordare che la (4.1) esprime la relazione fra le componenti dell’entropia in ogni stato della trasformazione nella ipotesi che l’entropia totale non sia una variabile indipendente, ma sia una funzione delle due variabili di stato p e v. Quindi, seguendo la teoria di Clausius, se ne trae che esistendo le due variabili di stato in ogni punto della trasformazione, deve esistere anche l’entropia totale e quindi anche le sue due componenti. L’applicazione della (4.1) alla trasformazione irreversibile del sistema isolato deve quindi comportare necessariamente a sinistra l’addendo (dq/T)i non come indicatore della quantità di calore in fase di assorbimento, ma come componente necessaria dell’entropia totale. Naturalmente deve comportare anche la presenza della componente dSi, ma la componente (dq/T)i può solo crescere man mano che diminuisce la componente dSi. Infatti. per la tendenza del calore al passaggio dalle zone calde alle zone fredde (postulato di Carnot-Clausius) si raggiunge gradualmente la condizione di completa omogeneizzazione del sistema e quindi la scomparsa della componente dSi, legata alle condizioni di disomogeneità del sistema. Quindi in un sistema isolato non potendosi verificare alcuna variazione delle variabili di stato (nell’ipotesi di un volume limitato) non può verificarsi alcuna variazione dell’entropia termodinamica totale; può solo verificarsi la scomparsa della componente dSi per la scomparsa dei disequilibri interni.
Con ciò non significa negare che in un sistema isolato, in cui esistano inizialmente condizioni di disequilibrio termico, quindi in uno stato provvisorio, determinato da una precedente condizione di non isolamento, tenda verso una condizione di equilibrio termico, cui corrisponde il valore massimo dell’entropia statistica che esprime appunto il livello di omogeneizzazione dello stato del sistema, ma questa è una condizione che deriva direttamente dal postulato di Carnot-Clausius, senza necessità di passare per il fantasioso ragionamento di Clausius. Per alcuni autori infatti la seconda legge della termodinamica coincide semplicemente con il postulato di Carnot Clausius. E’ però senza dubbio importante l’accento che l’introduzione delle trasformazioni reversibili ed irreversibili pone sulle modalità con cui la trasformazione termodinamica, basata sullo sfruttamento di un disequilibrio termico, viene eseguita, modalità che possono portare, in misura maggiore o minore, a movimenti interni dei flussi di calore che si riflettono sull’efficienza del processo produttivo.
6-Conclusioni
Non sono mancate nel passato le voci critiche della teoria di Clausius, sopratutto a partire dalla fine del diciannovesimo secolo, con i lavori di Poincaré [2] e Zermelo e poi, agli inizi del ventesimo secolo, di Paul e Tatiana Ehrenfest [3] e sulla stessa linea sono alcune considerazioni di Planck che non solo prospettavano l’esigenza di una terza variabile di stato, ma la caratterizzavano come un vincolo interno al sistema, così centrando pienamente il problema [4], lavori tutti rimasti inascoltati come addirittura ignorati erano rimasti i risultati di Pfaff [1].
La teoria della termodinamica derivata dalla formulazione di Clausius conduce in casi particolari ad evidenti paradossi, quale l’impossibilità di una formazione iniziale di ordine nelle Galassie, mostrata da Gott [9] o quello di Finkelstein [11] secondo cui, seguendo le leggi della termodinamica classica, si dovrebbero ottenere, in certi processi, temperature assolute negative.
E’ poi erronea l’estensione della teoria, anche nella formulazione statistica di Boltzmann, dai gas al più generale campo dei sistemi complessi, come appare, ad esempio, nel paradosso di Lamprecht [10] che ha mostrato che esistono processi biologici che mostrano riduzioni di entropia che sono certamente di origine endogena. Nel caso dei gas infatti non è possibile controllare la direzione dei disequilibri interni che si formano durante il processo trasformazionale in quanto il calore, trasportato dalle molecole del gas contigue alla sorgente, si diffonde lungo tutte le direzioni deviando continuamente per effetto degli urti. Occorre, al fine di controllare la direzione dei disequilibri, la formazione di strutture di rigidità che fungano da canalizzazioni, cioè, nei termini di Prigogine [5], il passaggio dalla fase termodinamica alla fase cinetica del processo trasformazionale. Nella fase termodinamica, non è possibile ricostruire e ripercorrere i percorsi svolti dai flussi di calore e le trasformazioni sono irreversibili, nella fase cinetica le strutture rigide introducono dei vincoli al movimento delle molecole e quindi dei flussi di calore e le trasformazioni possono divenire reversibili. Ma già i greci avevano capito che per rendere reversibile un percorso occorre un filo di Arianna; se il sentiero è segnato, ripercorrerlo in senso inverso non costituisce più un problema.
Nel caso più generale i sistemi complessi assumono un aspetto reticolare che consente l’indirizzamento dei flussi di energia nei nodi della rete.
Dunque, sia la teoria di Clausius che quella di Boltzmann, se applicate ai sistemi complessi, presentano il grave difetto di non tenere conto della direzione in cui i disequilibri interni si svolgono. Il disequilibrio interno sottrae energia al lavoro se la sua direzione è diversa da quella delle forze che producono lavoro, ma può invece aggiungere energia al lavoro se ha la stessa direzione. Il punto è estremamente importante perché è nel convogliare tutte le forze del sistema verso la resistenza esterna che consiste il nucleo fondamentale dell’organizzazione [5]. La diminuzione dell’entropia statistica può quindi avere effetti negativi o positivi sulla efficienza del sistema a seconda della direzione del disequilibrio che essa sottende.
Che le differenze fra le trasformazioni termodinamiche incontrate nelle applicazioni della seconda legge della termodinamica possano essere attribuite ad una variabile non ancora individuata, che tale soluzione abbia caratteristiche di grande semplicità e verosimiglianza, laddove invece la soluzione data da Clausius al problema dia luogo, quanto meno, a dubbi e perplessità, non poteva sfuggire a tutti gli scienziati che la hanno studiata nel corso di più di un secolo e mezzo dalla sua formulazione, così che in realtà l’accettazione ottenuta dalla teoria di Clausius, che viene ancora insegnata nelle università, potrebbe sembrare uno dei misteri della scienza.. A mio parere ciò è dovuto all’enorme peso che, dopo Galileo, viene dato alla conferma sperimentale così che , quando questa sussiste, non si dà più luogo a discussione e le capacità critiche si addormentano. Malgrado che nell’ambito della logica si dimostri che un risultato vero può scaturire da una successione di passaggi logici falsi, ciò non scalfisce la fede assoluta nella teoria.
L’apporto alla filosofia della scienza di Karl Popper, uno dei maggiori filosofi del ventesimo secolo, à stato principalmente centrato su questo argomento. Egli ha mostrato che, anche in presenza della conferma sperimentale, l’esistenza di errori nella catena dei passaggi teorici non solo ne limita la generalità, ma costituisce anche un ostacolo pesante all’ulteriore sviluppo della scienza. Egli ha quindi sostenuto che non occorre solo la conferma sperimentale, ma occorre il superamento di test di falsificazione, cioè studiati in modo di dirimere la validità di ogni passaggio elementare della teoria [14].
Ma, come abbiamo mostrato in questo studio, anche la attenta analisi matematica del processo logico può rivelare i punti deboli di una teoria, può, esprimendoci nel linguaggio di Popper, falsificarla, se ci si libera dalle costrizioni mentali dovute alla accettazione globale che possono trasformarla in una religione.
Riferimenti
[ 1] – Pfaff, in Abb.d. Ber. Acad. (f814,815),presentato alla Berlin Academy il 11 maggio 1815.
[ 2] – Poincaré H.: Revue de Metaphysique et de Morale, 1893
[ 3] – Ehrenfest P., Ehrenfest T.: Encyclopedia of Mathematics, 1911
[ 4] – Planck M.: Annln. Phys., 19, 759, 1934, Physica, 2, 1029, 1935
[ 5] – Prigogine I., Nicolis G.: Self-Organization in Non-equilibrium Systems, Wiley, New York, 1977
[ 6] – Einstein A.: Uber die Spezielle und Allgemeine Relativitats-theorie, Lipsia, 1916
[ 7] – Boltzmann I.: Wien. Ber., 76, 373, 1877, K,Acad. Wiss. Sitzb, II Abt. 66, 275, 1871
[ 8] – Firrao S.: On Boltzmann Statistical Entropy, Cybernetics and Systems, 5, 20, September 1989
[ 9] – Gott R.J.: Recent Theories of Galaxy Formation, Annual Review of Astronomy and Astrophysics, 15, 1977
[10] – Lamprecht I.:Thermodynamics of Biological Processes, Lamprecht and Zotin eds., de Gruiter, Berlin, 1978.
[11] – Finkelstein R.J:Thermodynamics and Statistical Mechanics Freeman, San Francisco, 1969, 147
[12] – Firrao S.: Development of Oscillatory processes in Isolated High Energy Systems Cibernetica, XXXI, 4, 1988
[13] – Firrao S.:La formazione dell’ordine nelle Galassie Studi sui Sistemi Complessi, 2011, ISBN 978-1-4476-3406-5, Lulu.com
[14] – Popper K.:Logica della ricerca scientifica,1934, Einaudi,Torimo, 1970
